Adaptive Symmetrization of the KL Divergence
An approach to non-adversarially minimize the symmetric Jeffreys divergence.
Introduction
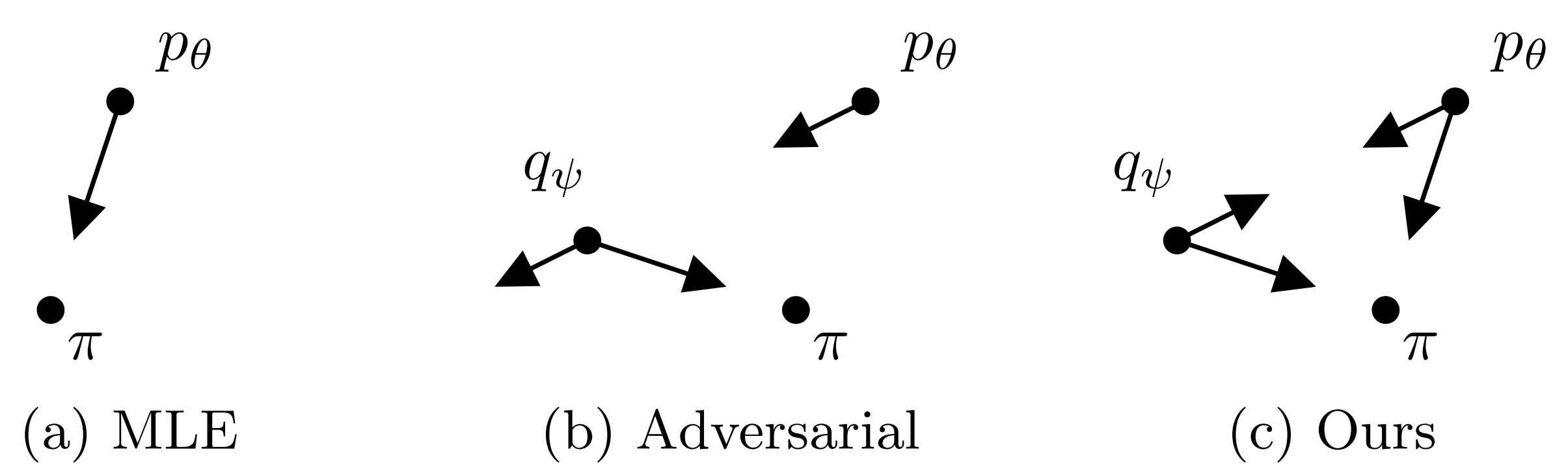
Many tasks in machine learning can be described as learning a distribution $\pi$ from a finite set of samples. The most widely used approach is to minimize a statistical divergence. A common divergence is the forward KL divergence, as it is equivalent to cross entropy, or maximum likelihood estimation (MLE). However, the KL divergence is not symmetric and may lead the trained model to overestimate the weight of modes (a behavior also known as mode-covering). While minimizing the reverse KL tends to a mode-seeking behavior, which can counteract the mode-covering of the forward KL, this minimization requires access to the distribution we are trying to learn, which is impossible when given only finite data samples.
GANs propose another approach to minimize a symmetric divergence based on variational representations, where an additional model is introduced to represent the divergence as an optimization problem. This approach results in a min-max objective that is unstable to train and sensitive to the choice of hyper-parameters.
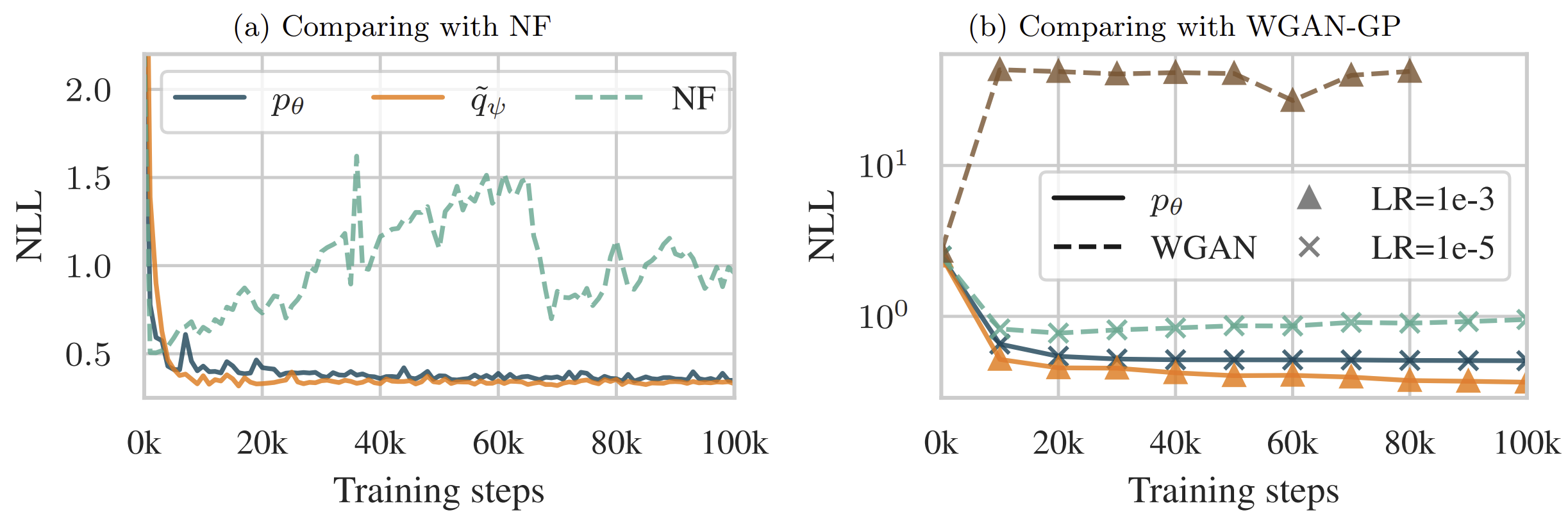
In this work, we propose to introduce an additional model to serve as a proxy to the true distribution $\pi$ and use it to approximate the reverse KL. By minimizing the sum of the forward and reverse KLs, also known as the Jeffreys divergence, we have both mode-covering and mode-seeking behaviors.
Resources
- For more details, results and limitations, please read our research preprint